2022.05.25 コラム
【テックコラム】 相関分析の可視化
<執筆者プロフィール>
岩浅 祥平 Iwasa Shohei
2019年サイバー・コミュニケーションズ(現:CARTA COMMUNICATIONS、略称「CCI」)入社し、DMP運用、MLサービス構築、ML勉強会講師などを主に行ってきた。2021年1月より株式会社DataCurrentに出向し現在は、機械学習プロダクト開発のDS領域担当、社内のDS文化の醸成、お客様のデータ分析業務に従事している。
● コラムのモチベーション(動機)
データを可視化することで見えてくる事が多いと言うことは周知の事実だと思います。しかし、いかんせん可視化手法はたくさんあるので、どのシーンでどの可視化手法を使えばよいか悩むケースは多いと思います。シーン別の可視化手法が整理されていると嬉しいのでは?というところがこのコラムのモチベーションになっております。 (※このコラムでは整理するところまでは至っていません!)
● はじめに(このコラムで話すことなど)
まずはどんな可視化手法があるのかを色々見ていきたいと思います。
ただし、分析の種類についてはさすがに絞らなければまとまりが悪すぎると思われますので、今回は相関分析に絞ろうと思います。
次に相関係数についてですが、相関係数にはいくつか種類があります。
一般的に使われることが多いのはピアソンの相関関係かなと思います。
このコラムで特に断り無く相関という言葉を使っている場合は、ピアソンの相関関係を指しています。
他には、スピアマンの順位相関係数や、ケンドールの順位相関係数などがあります。
また、可視化についてはGoogle Colaboratory 上で Python のライブラリである、seabornをメインに使っていきたいと思います。
● データセットの確認と準備
まずライブラリを読み込みます。Colaboratoryに入っていないライブラリはインストールしていきます。
!pip -q install japanize_matplotlib pyvis==0.1.9 import pandas as pd import numpy as np import matplotlib.pyplot as plt %matplotlib inline import seaborn as sns sns.set() import japanize_matplotlib from sklearn.datasets import fetch_california_housing import networkx as nx from pyvis.network import Network from IPython.display import HTML
主要なライブラリのバージョンを確認しておきます。
!pip freeze | egrep "seaborn|pyvis"
pyvis==0.1.9 seaborn==0.11.2
今回使うデータはこちらです。 日本語に翻訳したもので見ていきたいと思います。
California Housing dataset
データの内容について一部日本語に翻訳したものを転載します。
ターゲット変数はカリフォルニア州の住宅価格の中央値で、数十万ドル($100,000)単位で表示される。 このデータセットは、1990年の国勢調査から得られたもので、国勢調査ブロックグループごとに1行ずつ使用されている。ブロックグループとは、米国国勢調査局が標本データを公表している最小の地理的単位である(ブロックグループの人口は通常600~3,000人である)。 世帯とは、家庭内に居住する人々の集団のことです。このデータセットでは、1世帯あたりの平均部屋数と平均寝室数を提供しているため、別荘地など世帯数が少なく空家が多いブロックグループでは、これらの列が突出して大きな値を取ることがあります。
データを読み込みます。以降の見やすさのためカラム名は日本語に変換しておきます。
california_housing = fetch_california_housing()
df = pd.DataFrame(california_housing.data, columns=california_housing.feature_names)
df["HousePrice"] = pd.Series(california_housing.target)
df = df.rename(columns={
"MedInc": "所得中央値",
"HouseAge": "築年数中央値",
"AveRooms": "1世帯あたりの平均部屋数",
"AveBedrms": "1世帯あたりの平均寝室数",
"Population": "人口",
"AveOccup": "平均世帯人員",
"Latitude": "緯度",
"Longitude": "経度",
"HousePrice": "住宅価格",
})
df.head(10)
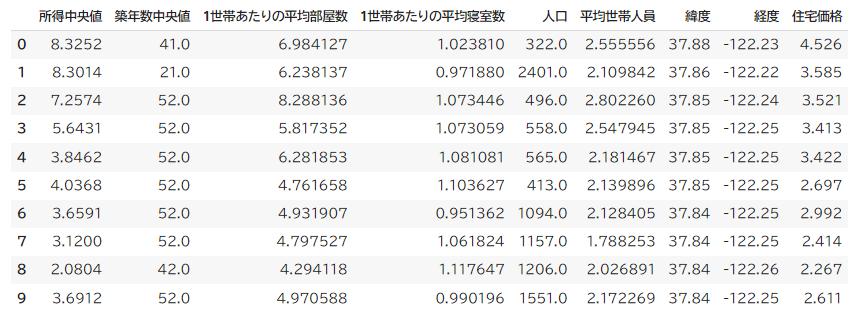
まず全体の傾向をヒストグラムで見てみます。(さっそくseabornではなく、Pandasのplotを使っていますがご容赦下さい。)
for col in df:
print(col)
df[col].plot.hist()
plt.show()
全カラム分出すと長くなりますので、「住宅価格」のヒストグラムだけ出しておきます。
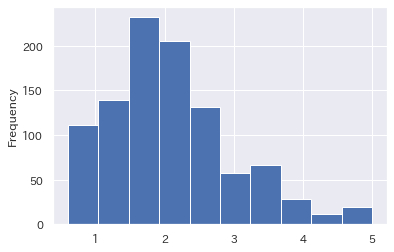
後の可視化のために住宅価格TOP100フラグを作成しておきます。
df["住宅価格top100"] = df.index.isin(df["住宅価格"].rank().sort_values().tail(100).index).astype(int)
● 散布図
まずはオーソドックスに散布図です。
散布図は2変数間の関係性を確認することができます。
相関係数の詳細はwikipediaに譲りますが、2変数間に線形関係が見られる場合に相関係数は高くなります。線形ではないものの、明らかに何かしらの特徴が見られても相関係数の数値だけを見ているとそれに気付けません。そういった事があり得るので散布図で視覚的に見ておくことは重要かなと思います。
plt.figure(figsize=(10,10)) sns.scatterplot(data=df, x="所得中央値", y="住宅価格")
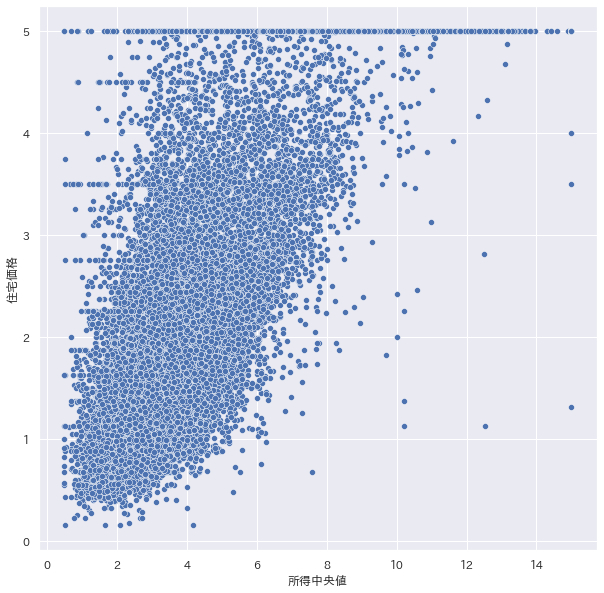
若干ですが正の相関があるように見えます。可視化するにはレコード数が多いので次からは少しサンプリングして行きます。
sample = df.sample(1000, random_state=0).reset_index(drop=True)
ここからはseabornの見た目も少し考慮して、所得と部屋数を見ていきます。 hueを使う事で3つの変数の関係性を見ることができます。
plt.figure(figsize=(10,10)) sns.scatterplot(data=sample, x="所得中央値", y="1世帯あたりの平均部屋数", hue="住宅価格top100", s=60, alpha=.7)
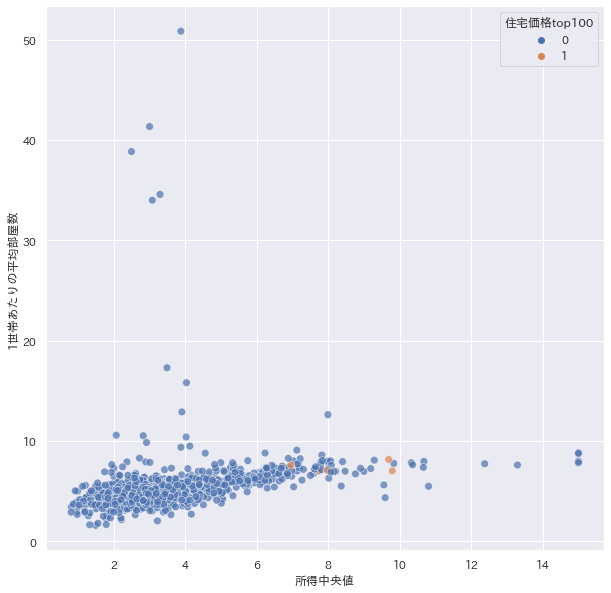
上部の方を見ると部屋数が異常に多い住宅があるようです。部屋数が多い=住宅価格が高いわけでもなさそうです。またピアソンの相関係数は外れ値の影響を強く受けるので除外するのも一つの手かもしれません。
所得と築年数の関係も見ていきます。
plt.figure(figsize=(10,10)) sns.scatterplot(data=sample, x="所得中央値", y="築年数中央値", hue="住宅価格top100", s=60, alpha=.7)
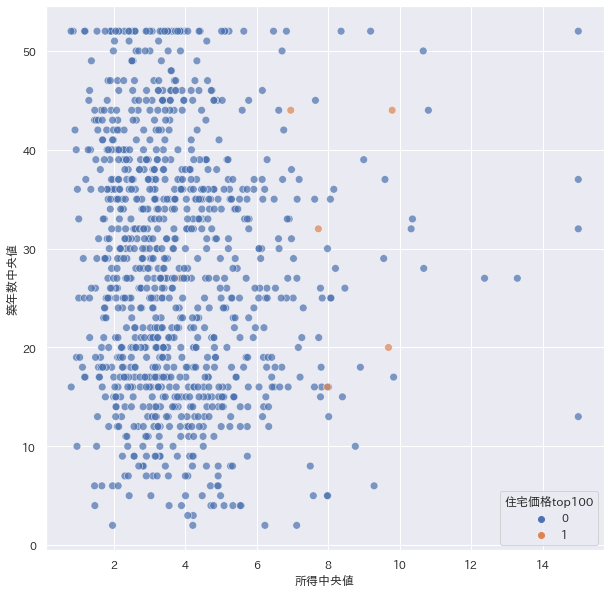
やはり所得が高い人達はtop100の住宅に住んでいる傾向があるように見えますね。ただ築年数と所得には関係性はないようです。
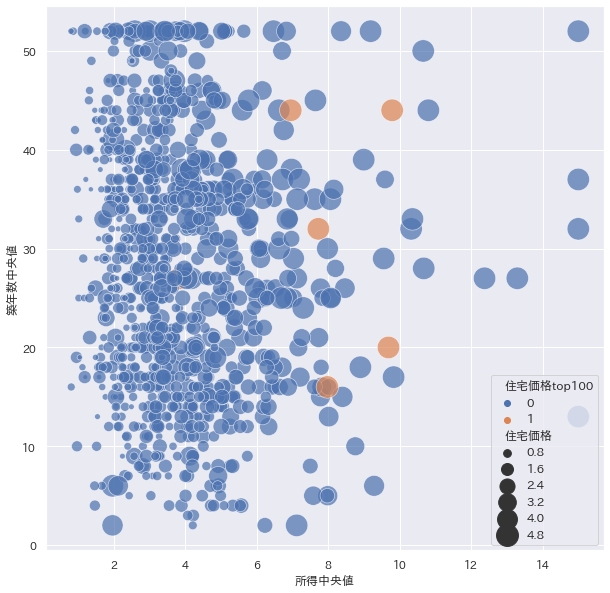
● バブルチャート
散布図の応用みたいなところでバブルチャートがあるかと思います。 2変数間のプロットをするところは散布図と同じですが、プロットした点に大きさを持たせます。 一つ前の図と見比べるとこちらのほうが得られる情報が多いことが分かります。
plt.figure(figsize=(10,10))
sns.scatterplot(
data=sample, x="所得中央値", y="築年数中央値", hue="住宅価格top100", size="住宅価格",
sizes=(10, 500), s=60, alpha=.7
)
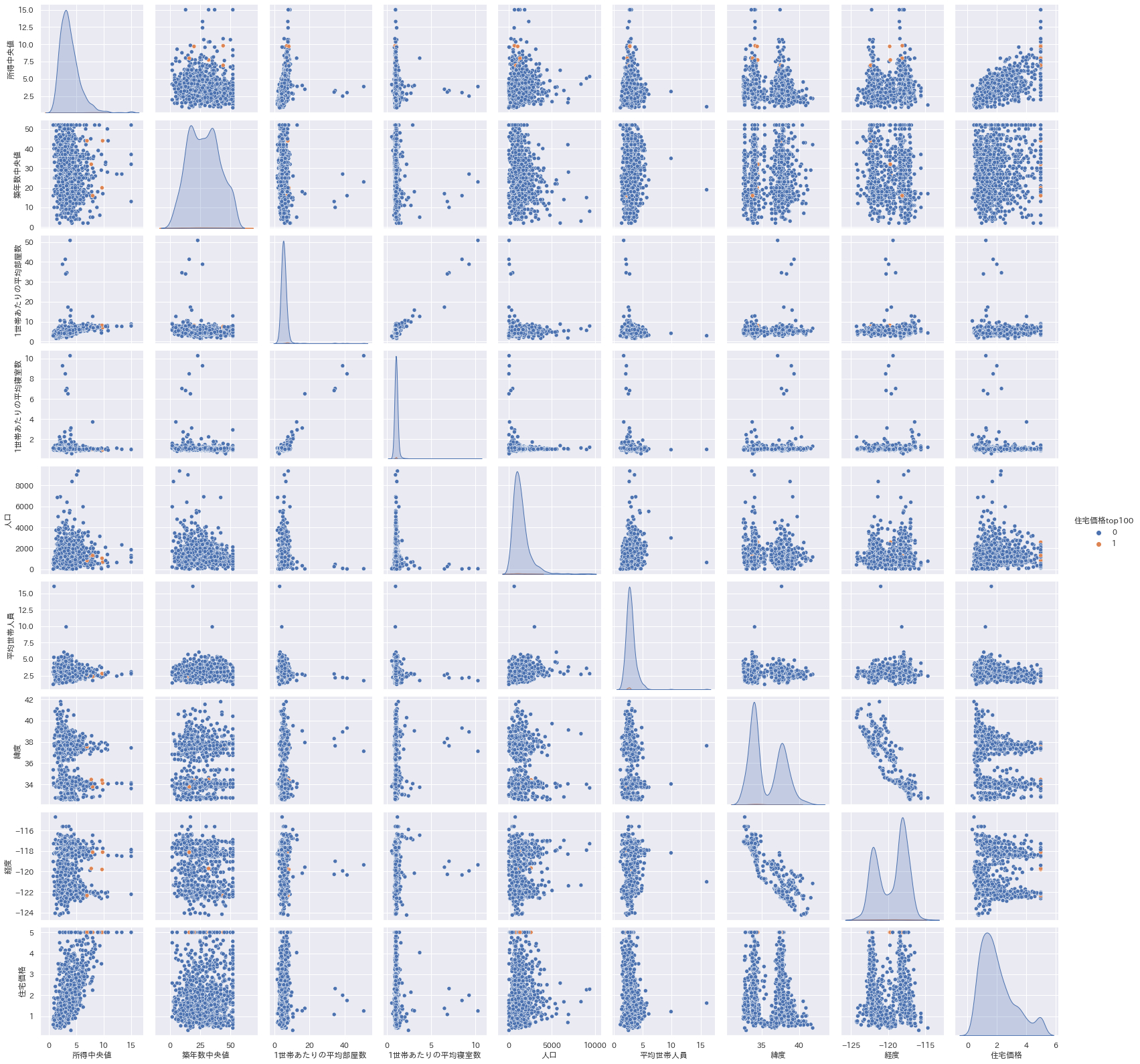
● ペアプロット
データの変数の数が多い場合はペアプロットという可視化ができますseabornのペアプロットを使う事が多いですが、ラベル別に色分けしてくれたり、対角線は完全な相関があるため表示する意味がないのでそこにヒストグラムを表示してくれたりします。ラベルがある場合はラベル別のヒストグラムを出力できるので概観するのによく使います。
plt.figure(figsize=(10,10)) sns.pairplot(sample, hue="住宅価格top100", height=2.5)
● ヒートマップ
これまではグラフを見てきましたが、2変数間の相関係数を計算して相関行列を作る事も多いです。
例えばこのようなものですが、相関計数の値によって色を付けてくれますので、これも概観する時に便利です。データの変数の数が多い場合には特に有用かと思います。
plt.figure(figsize=(10,10))
options = {'square':True, 'annot':True, 'fmt':'0.2f', 'xticklabels':df.columns, 'yticklabels':df.columns, 'annot_kws':{'size':12}, 'vmin':-1,'vmax':1,'center':0, 'cbar':False}
ax = sns.heatmap(df.corr(), **options)
ax.tick_params(axis='x', labelsize=24)
ax.tick_params(axis='y', labelsize=24)

● グラフネットワーク
最後にあまり例を見ることが少ないのですが面白い可視化を紹介したいと思います。よくSNS分析などの文脈で登場するかと思われます。まずはどのようなものか見てみましょう。
threshold=0.4
edge_width=10
df_corr = df.corr()
mask_df = df_corr.mask(np.triu(np.ones(df_corr.shape)).astype(bool), None) # 「右上の三角行列」にマスクをして、Noneに置き換える
# edges data frame
edges = mask_df.stack().reset_index().rename(columns={"level_0":"source", "level_1":"target", 0:"weight",})
# edges = edges.loc[abs(edges['weight'])> threshold] # 該当のノードのみ出したい場合コメントアウト外す
edges['width'] = edges['weight'].apply(lambda x: abs(x) * edge_width if abs(x) > threshold else 0) # weightに応じて、エッジの太さを変更
edges['color'] = edges['weight'].apply(lambda x: '#33A5CC' if x>threshold else '#BD4141') # edgeの色
edges['label'] = edges['weight'].apply(lambda x: np.round(x,2) if abs(x) > threshold else '')
# networkxからpyvisに変換
G = nx.from_pandas_edgelist(edges, edge_attr=True)
nt = Network(height=f'1000px', width=f'1000px', bgcolor="#FFFFFF", font_color="black", notebook=True, directed=False) # heading='test graph',
nt.from_nx(G)
# グラフ構造
nt.repulsion(node_distance=300)
# ノードのレイアウト
neighbor_map = nt.get_adj_list()
for n in nt.nodes:
n['font'] = {'size':20, 'strokeWidth':6}
n['size'] = 15 # shapeの内部にラベルがないノード形状のサイズ
# エッジのレイアウト
for e in nt.edges:
if e['weight'] >= threshold:
e['font'] = {'size':30, 'strokeWidth':10, 'color': '#33A5CC'} # strokeWidth: weightの背景範囲
else:
e['font'] = {'size':30, 'strokeWidth':10, 'color': '#BD4141'}
nt.show_buttons(filter_=['physics'])
nt.show("tmp.html")
display(HTML("tmp.html"))
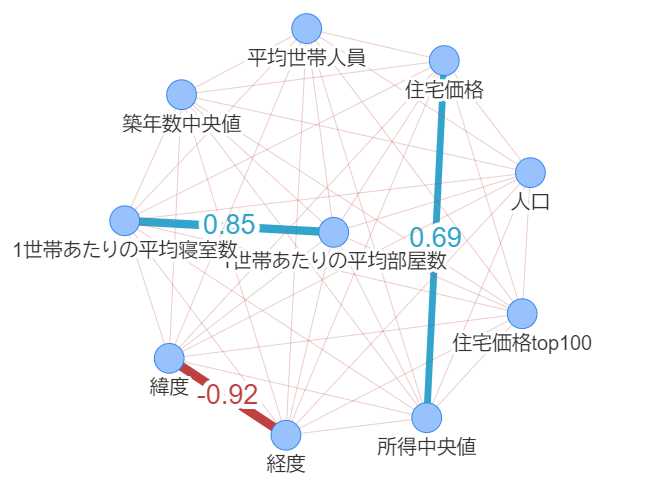
これがグラフネットワークと呼ばれるもので、エッジ(線)とノード(点)で構成されています。作り方は、まず相関行列を作ります。相関行列の行と列のインデックスがノードにあたります。全ての組み合わせが存在するので、上のように各カラムが全結合している形になります。そして、このグラフでは相関係数が0.4より大きいエッジを強調しています。つまり住宅価格と取得は相関関係が少しあるという見方が出来ます。負の相関の場合は赤で表現させています。
また今回のような変数の数であれば上のようなグラフで良い気もしますが、変数がもっと多い場合は9行目のコメントアウトを外していただくと、以下のように表現する事も出来ます。
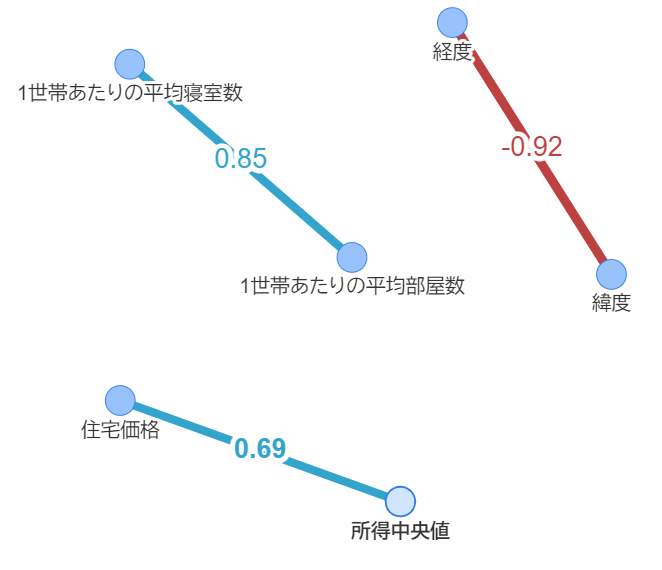
ここまで色々見てきましたが、どれも必要なシーンで使い分けて使っている気がします。シーン別に可視化手法をまとめるにはどうすればよいかについては次回検討したいと思います。ということで本コラムはここまでにしたいと思います。最後まで見ていただきありがとうございました。
● 最後に
自社に専門人材がいない、リソースが足りない等の課題をお持ちの方に、エンジニア領域の支援サービス(Data Engineer Hub)をご提供しています。
お困りごとがございましたら、是非お気軽にご相談ください。

本記事に関するお問い合わせは下記にて承ります。
株式会社DataCurrent
info@datacurrent.co.jp
