2021.11.12 コラム
【テックコラム】データ活用!相関関係と因果関係の違いと擬似相関について
● はじめに
こんにちは、DataCurrentの岩浅です。
データ同士の関係性を把握したいケースは多々あるかと思います。(例えば、ある広告施策と売上の関係性など)
そういう時、回帰分析や相関分析を行うと思いますが、その中で相関関係は因果関係とは異なるという話がよく出てきます。これは、ある2つのデータの相関関係を見た時、(統計的にも有意に)相関関係が見られるが、その2つのデータには因果関係があるとは限らないから注意しましょう、という話です。
代表的な例として各国のチョコレートの消費量とノーベル賞の受賞者数の相関を調査したものがあります。
下の図を見ると正の相関がある事が分かります。(横軸がチョコレートの消費量、縦軸がノーベル賞受賞者数)
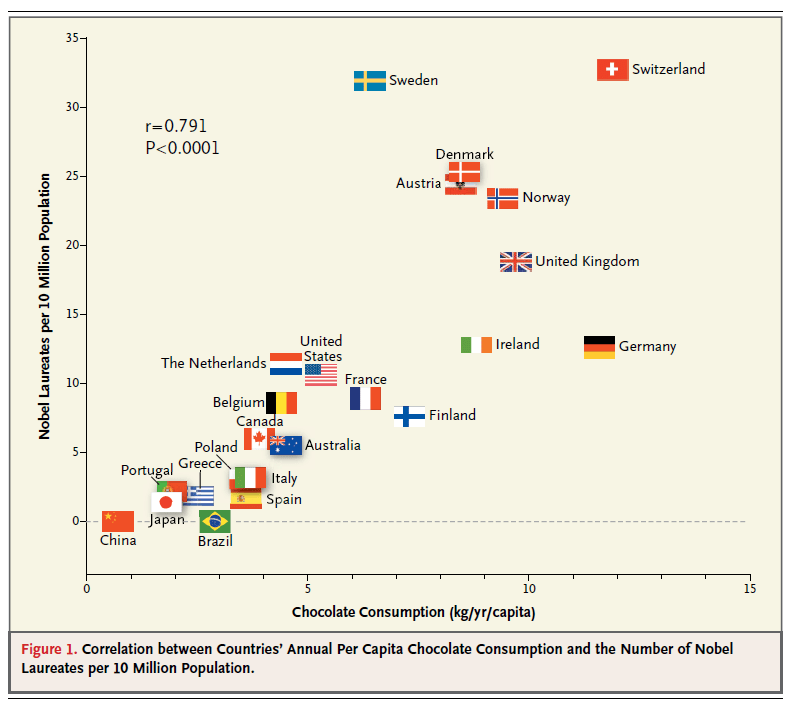
この調査結果を安易に解釈すれば、チョコレートを多く食べれば、ノーベル賞が取りやすくなるといった感じでしょう。本当にそうでしょうか?
この例は極端ですが、リアルな現場でもこのような分析結果の解釈がされているケースは少なくないと想像できます。それは一見、解釈がもっともらしいと感じるケースが多いからだと思います。この例の場合、脳は糖分をエネルギー源とするので頭の良い人は糖分を多くとっているのでは?といった連想が出来るので、それをもっとらしいと感じるといった具合です。
本記事では、こういった分析結果の安易な解釈をしてしまう事を避けるために、相関関係と因果関係の違いや関係性を把握する事を目的とします。
また本記事では取り上げませんが、因果関係の理解は、因果推論や因果探索の前提知識になります。
因果推論や因果探索はマーケティング等で、施策の効果を予測したい場合や、データから因果関係を予測したい場合に扱う技術です。ご興味がある方はまずは本記事の内容ついて理解をしておきたいところです。
● 目次
- 相関関係と因果関係とは
- 相関関係と因果関係の関係
- 疑似相関とは
● 相関関係と因果関係とは
まずは相関関係と因果関係についてそれぞれの特徴を簡単に説明します。ここでは数式等を伴う詳細の説明は省略します。
相関関係
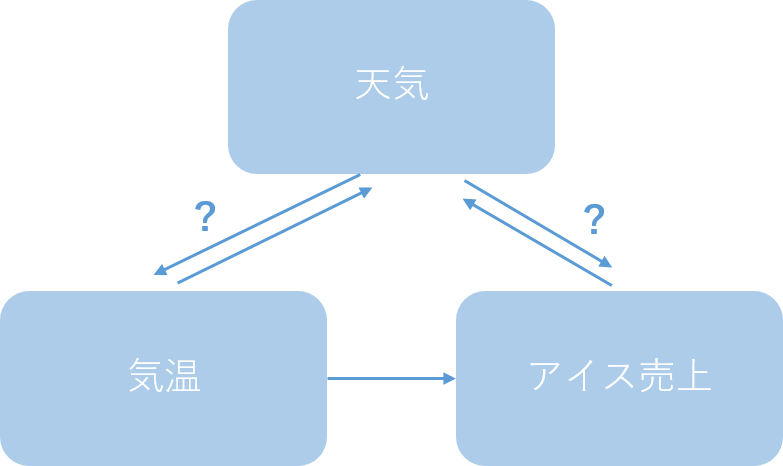
まず相関係数ですが、2つのデータ(変数)の関係性の強さを表します。2つのデータを下図のように縦横の軸としてプロットした時に、片方が増えた時、もう片方も増えているような関係性がある時、正の相関があるといい、右肩上りになっているのが分かります。負の相関というものもあり、右肩下がりになります。これは片方が増加した時、もう片方は減少しているような関係性を持ちます。例えばアイスの売上と気温の関係を考えてみます。気温が上がれば売上も上がるため正の相関があると想像できます。下図に当てはめて見ると想像できるのではないでしょうか。
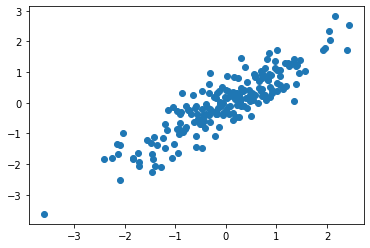
一方、下図は上の例のように右肩上りでも右肩下がりでもありません。これは相関が無い状態です。
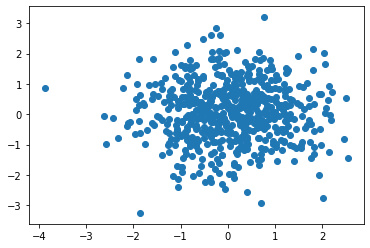
因果関係
次に因果関係ですが、2つのデータ(変数)が原因と結果で繋がっている関係性の事を指します。 簡単に図にしてみると下記のような関係です(因果グラフと呼びます)。ここで重要な事は矢印の方向です。原因から結果に向かって矢印が引かれていますが、これは原因から生じる結果であって、その逆(結果から原因が生じるわけではない)はないと言うことです。
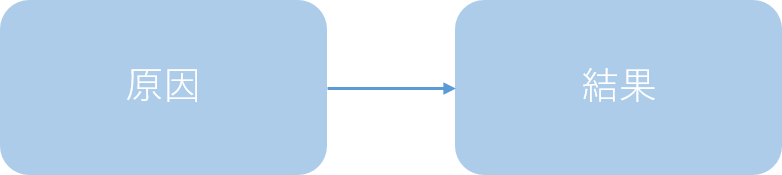
アイスの売上と気温の例の場合、気温が原因で、アイスの売上が変化する事はその通りですが、その逆(アイスの売上が原因で気温が変化する事)はおかしい事は自明だと思います。
● 相関関係と因果関係の関係
アイスの事例で、相関関係と因果関係を見てきましたがこれらにどんな関係があるでしょうか。上のアイスの例を整理してみます。
- アイスの気温と売上に相関関係があり、気温→売上に因果関係はある
- アイスの気温と売上に相関関係があり、気温←売上に因果関係は無い
※矢印の向きに注意
つまり、相関関係があっても因果関係が無いケースがあるという事です。こういった現象は擬似相関と呼ばれます。疑似相関は「見せかけの相関」とも呼ばれる事もあるようです。
ちなみに「見せかけの回帰」という言葉がありますが、擬似相関とは異なるものになります。ここでは詳細は説明しませんが、見せかけの回帰は時系列データで回帰分析を行う際に、無関係な変数同士が有意に相関関係があるという結果が出てしまう問題です。
<複数の説明変数を扱うケースも考える必要がある>
上のアイスの例では、1つの説明変数と目的変数の関係性だったので簡単でしたが、実際に分析する場合は、複数の説明変数と目的変数の関係や、説明変数同士の関係を調べる事が多いと思います。
アイスの例で説明変数が2つのケースを見てみます。例えば、説明変数として「天気」を追加すると下図のようになりますが、天気が気温に与える影響や、売上に与える影響を考える必要が出てきます。このように3つ以上のデータの因果関係において発生する擬似相関もあります。
● 疑似相関とは
最後に代表的な擬似相関のパターンをいくつか見ていきます。擬似相関の説明に入る前に少しおさらいしておきます。
<おさらい>
改めて擬似相関を簡単に説明すると、相関関係はあるが因果関係が無い状態の事です。因果関係は原因と結果の関係の事を指し、見方を変えれば、ある変数Aが変化した時、対応する別の変数Bが変化する関係です(A:気温→B:売上といったように矢印が引かれる関係とも言える)。
それでは代表的な擬似相関のパターンを見ていきます。
パターン1:因果の関係が逆
これは今まで説明してきたアイスの例がそれにあたります。以下再掲します。
アイスの気温と売上に相関関係があり、気温←売上に因果関係は無い
気温が変化した時、アイスの売上が変化するが、アイスの売上が変化した時、気温は変化しない。その理由は擬似相関の一つである因果の関係が逆であるため。 と解釈できます。

パターン2:交絡因子
冒頭で見た、各国のチョコレートの消費量とノーベル賞の受賞者数を例として見ていきます。
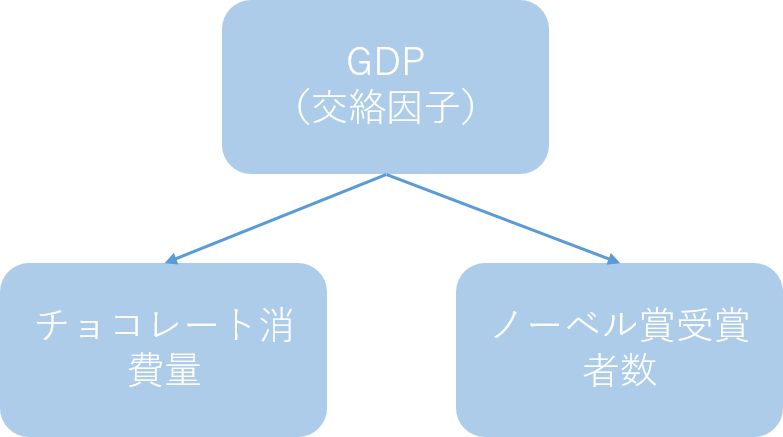
この例で、下図にあるように実はチョコレートの消費量とノーベル賞受賞者数には因果関係が無く、第3の変数である、「GDP」が両方に影響を与えていたというケースで考えます。因果関係が無いので、チョコレート消費量を増加する施策を行っても、ノーベル受賞者数は増加しません。ただし、GDPが増減すれば、チョコレートの消費量とノーベル賞受賞者数の両方も同じように増減するため、相関関係はあると見えてしまいます。このように第3の変数である「GDP」は、交絡因子と呼ばれます。交絡因子は見えていない事が多いため、交絡因子を無視した分析結果の解釈をしてしまう事が多いと想像できます。
パターン3:合流点バイアス
最後に、選択バイアスとも呼ばれる、バイアスがかかったデータが原因で擬似相関が発生するケースを見ていきます。少し理解しづらいので例を中心に説明していきます。
あなたは分析者です。ある大学受験の成績データの分析依頼を受けました。まずデータを散布図にしてみたところ、文系科目と理系科目に負の相関が見られるようです。
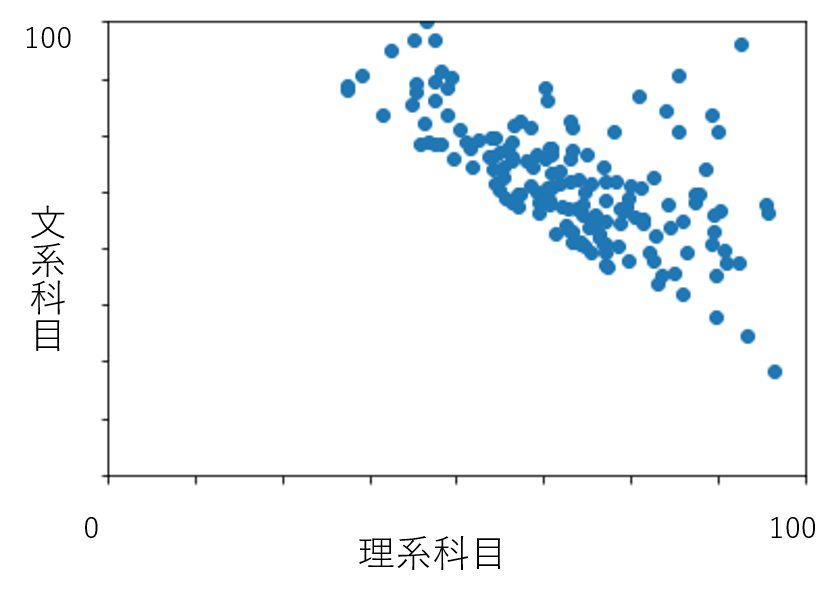
理系科目のが得意な人は、文系科目は苦手と考えれば、なんとなく納得感はありますが、片方の科目に偏り過ぎるようにも見えます。そこで依頼主にこのデータが作られた経緯を確認したところ、実は両科目の合計が130点以上(合格者)の人だけを抽出したものでした。
元の全体のデータを散布図を見ると(下図)、相関が無い事が分かります。また因果関係については、片方の科目の点数が原因で、もう片方の科目の点数が変化する事も考え難いです。
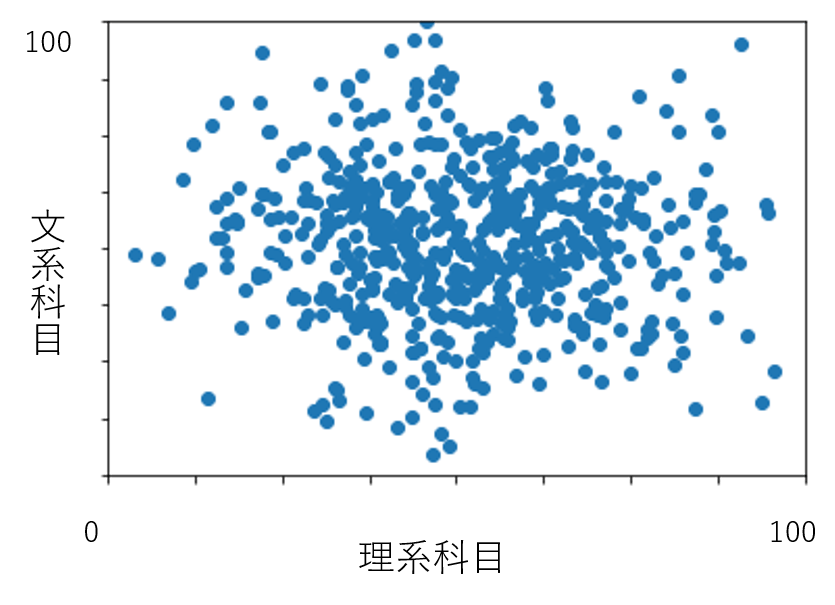
このように、全体(母集団)から何かしらの思惑により抽出されたデータが全体の傾向とは異なる時、抽出されたデータは選択バイアスがかかっているなどと表現します。
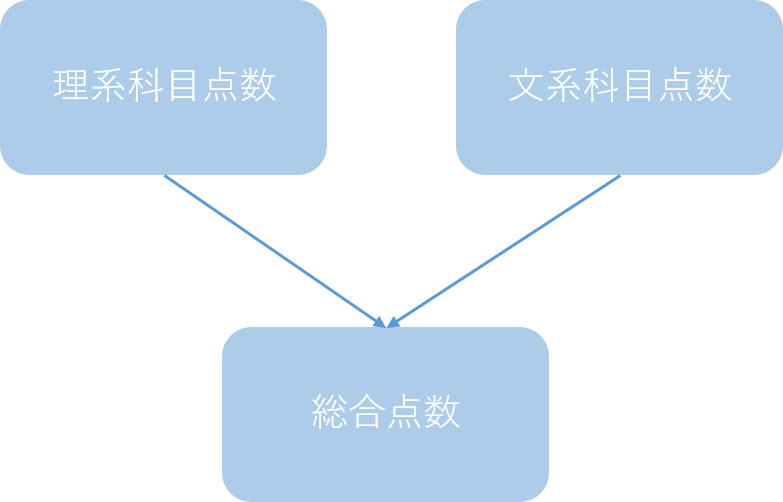
因果グラフにして整理すると、下図のように実際には理系科目の点数と文系科目の点数には相関関係もなければ因果関係もないのだが、合流点バイアス(選択バイアス)により相関関係があるように見えてしまうケースがあるという事です。
●さいごに
データ同士の関係性を把握したい場合に、相関関係は分析するコストも低いし分かりやすいですが解釈を誤ると、大きな施策を行ったが売上が全然上がらないといった事が起こり得ます。擬似相関の原因となる3パターンを見てきましたが、実はたまたま相関関係が見られるというケースもあります。いずれにしても回帰分析や相関分析を行った後、データ間の因果関係に意識を向ける事が大事だと思います。
今回は相関関係と因果関係の違いというお題で、因果関係の重要さをご紹介しました。データに関する課題がありましたら、お気軽にご相談ください。
また、自社に専門人材がいない、リソースが足りない等の課題をお持ちの方に、エンジニア領域の支援サービス(Data Engineer Hub)をご提供しています。
お困りごとがございましたら、是非お気軽にご相談ください。

