2021.06.28 コラム
【テックコラム】時系列データの基礎と可視化
● はじめに
こんにちは、DataCurrentの岩浅です。
時系列データを扱うことが多いので簡単に整理してみます。
時系列データは特に可視化が重要だと思うのでグラフを交えて説明していきます。
今回はPythonをベースに統計解析ツールである、statsmodelsと、可視化ツールであるplotlyを使っていきます。
(執筆時のバージョン:Python 3.7.10、plotly 4.4.1、statsmodels 0.12.2)
また使用したソースコードを掲載します。ライブラリの説明は今回は行いませんが、誰かの参考になれば幸いです。(扱うデータによって適当な関数や引数は異なりますので、誤った計算結果から誤った解釈をしてしまうといった点にはご注意ください)
● 時系列データ
時系列データとは
等間隔で記録されたデータで、前後に関係性が見られる事が特徴です。例えば1時間毎の気温は時系列データです。ちなみに、この例の「1時間毎」というのは観測者が決めているわけですが、これも時系列データの特徴と言えるかと思います。つまり、地震データのように観測者で決められないデータは時系列データではないとされています。
本コラムで扱うデータ
e-Stat(政府統計)のデータを見ていきたいと思います。
家計調査 家計収支編 二人以上の世帯
世帯区分: 二人以上の世帯(2000年~)
品目分類(総数:数量): ビール
時間軸: 月次
データ数: 436
つまり、二人以上の世帯の月次のビール消費量を見ていこうというわけです。
ビールの単位をリットルからミリリットルに変換します(特に意味は無いのですがビールの量を想像しやすいのでは、という意図です)
始めの数件を見てみます。(PandasのDataFrameを使っていますが、コードは省略します)
| amount | |
|---|---|
| date | |
| 2000-01-01 | 2510.0 |
| 2000-02-01 | 2880.0 |
| 2000-03-01 | 3540.0 |
| 2000-04-01 | 3790.0 |
| 2000-05-01 | 4480.0 |
次にグラフで確認します。
import plotly.graph_objects as go
import plotly.express as px
fig = px.line(df, x=df.index, y='amount')
layout = go.Layout(
width = 1000, height=600,
# title="beer",
xaxis=dict(nticks=50, tickformat="%Y-%m", title="年月", tickangle=45),
)
fig.update_layout(layout)
fig.show()
● 自己相関(Autocorrelation)
始めに自己相関について説明します。2つの変数間の関係性を表す相関係数がありますが、
自己相関(係数)は、1つの変数において、現在の自分と過去の自分の相関係数を計算します。
具体的には、下記表のイメージです。
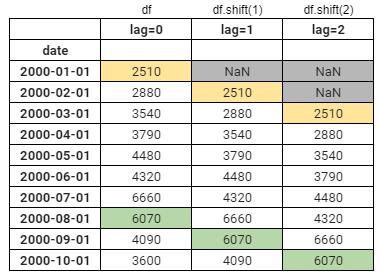
date列があり、lag=0,1,2列が続いていますが、lag=0が元のデータを表し、lag=1が1つ過去のデータです。
過去のデータというのが少しイメージし辛いですが、2000/2/1が現在だとして、その行のlag=1の値を見ると2000/1/1の値になっている事が分かると思います。
このようにズラす事をlag(ラグ)と呼びます。2つずらすならlag=2という事です。
Pandasではshift関数を使います。(df.shift(1))
元のデータ(lag=0)とlag=1の相関関係を求めた結果を、lag1の自己相関係数と呼んだりします。
ちなみにずらしたことにより”NaN”となってしまった行は補完する事も可能ですが、削除する事が多いと思います。
そして、lag=1の自己相関係数は、1か月前の自分とどれくらい相関があるかという意味があります。
● コレログラム
次にlag=2,3… とlagを増やしていったとき、自己相関係数がどのようになるかグラフで確認してみます。
横軸がlag、縦軸が自己相関係数のこのグラフは、コレログラムと呼ばれています。(ソースコードはこの後いくつかの説明の後に掲載します)
lagを1から80まで変えた時の元データとの相関関係をグラフ化したものです。網掛けの部分は95%信頼区間を表しています。簡単に言えば網掛け内は相関係数が0である可能性が高いという事です。
グラフの見方ですが、lag=0 の自己相関係数が1なのは、元データ同士の相関係数のためです。次にlag=12,24,36…と12の倍数で山が出来ています。つまりこのデータは12か月の周期性がありそうと解釈できます。
別の見方をすれば、ビールは夏に多く消費され冬はそれに比べ減少すると想像できますが、そういった傾向が毎年(12か月の周期性)ありそうと解釈できます。
● 偏自己相関(Partial autocorrelation)
自己相関のコレログラムから12か月周期がありそうと見ましたが、さらに正確に見るなら、偏自己相関も確認します。
先ほどの自己相関は、例えば、今月と先々月の自己相関を見たい時に、実は先月との関係性が含まれています。偏自己相関は、先月との関係性を取り除き、今月と先々月の直接的な関係を確認する事が出来ます。
こちらが偏自己相関のコレログラムになります。
lag=0,1は自己相関と同じになります。lag=0は自己相関と同じですが、lag=1の場合は間に値がないので関係性を取り除く必要がないため自己相関と同じになります。
lag=2,3を見ると自己相関のコレログラムと比べ小さい事が分かります。
これは、lag=1や2の関係性が取り除かれている事が分かります。
次にlag=12をみると相関がある事が分かります。今回のデータではやはり12か月周期のようだと解釈ができます。
自己相関と偏自己相関の計算と可視化のソースコードです。
from statsmodels.tsa.stattools import acf, pacf
autocorrelation, confint, qstat, pvalues = acf(df['amount'], nlags=80, qstat=True, fft=False, alpha=.05, missing='none')
p_autocorrelation, p_confint = pacf(df['amount'], nlags=80, method='ywmle', alpha=.05)
import plotly
import plotly.graph_objects as go
def plot_autocorrelation(autocorrelation, p_autocorrelation, confint, p_confint):
# fig & layout
fig = plotly.subplots.make_subplots(2,1, shared_xaxes=True, vertical_spacing=0.02, x_title='rag')
xasises = dict(showgrid=True)
layout = dict(margin=dict(l=50, r=50, t=100, b=50, autoexpand=True),
height=700, width=800,
title='Autocorrelation',
bargap=0.15,
bargroupgap=0.1,
xaxis=xasises, xaxis2=xasises,
)
fig.update_layout(layout)
# trace
tr1 = go.Bar(x=np.arange(len(autocorrelation)), y=autocorrelation, name='ACF', width=.5)
tr2 = go.Bar(x=np.arange(len(p_autocorrelation)), y=p_autocorrelation, name='PACF', width=.5)
tr3 = go.Scatter(x=list(range(len(confint))) + list(range(len(confint)))[::-1],
y=np.concatenate([np.array(confint)[:,0]-autocorrelation, (np.array(confint)[:,1]-autocorrelation)[::-1]]),
fill='toself', fillcolor='rgba(0,100,80,0.2)', line=dict(color='rgba(255,255,255,0)'), hoverinfo="skip", showlegend=False
)
tr4 = go.Scatter(x=list(range(len(p_confint))) + list(range(len(p_confint)))[::-1],
y=np.concatenate([np.array(p_confint)[:,0]-p_autocorrelation, (np.array(p_confint)[:,1]-p_autocorrelation)[::-1]]),
fill='toself', fillcolor='rgba(0,100,80,0.2)', line=dict(color='rgba(255,255,255,0)'), hoverinfo="skip", showlegend=False
)
# append fig
fig.append_trace(tr1, 1, 1)
fig.append_trace(tr3, 1, 1)
fig.append_trace(tr2, 2, 1)
fig.append_trace(tr4, 2, 1)
fig.show()
plot_autocorrelation(autocorrelation, p_autocorrelation, confint, p_confint)
● 時系列データの構成要素と成分分解
ここからは時系列データの構成要素について見ていきます。
時系列データは以下の3つの成分から構成されています。
・トレンド成分
・季節成分
・誤差成分
また誤差は、ホワイトノイズ(意味のない雑音)と外因性(外部の要因)から成ります。
元の時系列データから、3つの成分に成分分解してくれるライブラリがあるので、早速見ていきます。
import plotly
import plotly.express as px
from plotly import tools
from statsmodels.tsa.seasonal import STL
from statsmodels.tsa.seasonal import DecomposeResult
def plot_decompose(dc: DecomposeResult):
"""
dc = sm.tsa.seasonal_decompose(data.dropna(), model=model, freq=freq)
plot_decompose(dc)
"""
# fig & layout
fig = plotly.subplots.make_subplots(4,1, shared_xaxes=True, vertical_spacing=0.02, )
xasises = dict(nticks=50, tickformat="%Y-%m", tickangle=45)
layout = dict(margin=dict(l=0, r=0, t=0, b=0, autoexpand=True),
height=800, width=1200,
# title='decompose plot',
xaxis=xasises, xaxis2=xasises, xaxis3=xasises, xaxis4=xasises,
)
fig.update_layout(layout)
# trace
tr1 = go.Scatter(x=dc.observed.index, y=dc.observed, name="元のデータ", mode='lines+markers')
tr2 = go.Scatter(x=dc.trend.index, y=dc.trend, name="トレンド", mode='lines+markers')
tr3 = go.Scatter(x=dc.seasonal.index, y=dc.seasonal, name="季節性", mode='lines+markers')
tr4 = go.Scatter(x=dc.resid.index, y=dc.resid, name="誤差", mode='lines+markers')
# append fig
fig.append_trace(tr1, 1, 1)
fig.append_trace(tr2, 2, 1)
fig.append_trace(tr3, 3, 1)
fig.append_trace(tr4, 4, 1)
fig.show()
dc = STL(df['amount'], period=12, robust=True).fit()
plot_decompose(dc)
上から、元データ、トレンド成分、季節性成分、誤差成分のグラフになっています。
トレンドを見ると下降トレンドである事が分かります。季節性を見ると7,8月は消費量が多い事が分かります。
個人的に予想外だったのは12月が7,8月に次いで消費量が多い事です。正月前に買い溜めするのか、など次の分析の仮説を考える材料にもなりそうです。最後は誤差ですが、ちょこちょこ値が大きくなったり小さくなっていたりします。例えば2019/9など何かしらの外因性があったのかと調べると何か見つかるかもしれません。
このような3成分ですが、実は足し合わせると元のデータになります。(縦軸の値を見れば分かるかと思います)これを加法モデルといいます。その他には掛け合わせで構成される乗法モデルというのもあります。今回はSTLという手法で成分分解してみましたがSTLでは加法分解の機能の提供のみのようです。
statsmodels.tsa.seasonal.STL — statsmodels
● さいごに
時系列データについて、自己相関、偏自己相関、成分分解をグラフを交えて説明してきました。
今回便利なライブラリをいくつか使いましたが、その仕組を理解していないと誤った解釈をしてしまう恐れがあるのでご注意ください。また今回扱ったデータは季節性やトレンドが分かりやすいものでした。実務における時系列データは、分析する前にデータが欠損していたり外れ値があるなど、考慮しなくてはいけない事が多くあります。そして今回は時系列データの特徴を分析しましたが、その特徴を元に時系列モデルを構築し、過去データから将来の予測を行うも出来ます。時系列データを含むデータ活用の課題がありましたら、お気軽にご相談ください。
